Relasi matematika yaitu hubungan antara anggota pada suatu himpunan dengan anggota himpunan yang lainya. Relasi dari himpunan A ke himpunan B ialah menghubungkan anggota-anggota himpunan A pada anggota-anggota himpunan B. Dan terdapat jenis relasi, diantaranya seperti Relasi Refleksif, Irefleksif, Simetrik, Anti-simetrik dan Relasi Transitif
Pada relasi, tidak ada aturan khusus untuk memasangkan setiap anggota himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas pernyataan relasi tersebut. Setiap anggota himpunan daerah asal boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan.
Penyataan Relasi
Relasi menyatakan hubungan antara suatu anggota himpunan dengan anggota himpunan lainnya. Himpunan A dan himpunan B dikatakan memiliki relasi jika ada anggota himpunan yang saling berpasangan. Relasi antara dua himpunan dapat dinyatakan dengan tiga cara yaitu dengan diagram panah, himpunan pasangan berurutan, dan diagram Cartesius.
Diagram Panah
merupakan cara yang paling mudah untuk menyatakan suatu relasi. Diagram ini membentuk pola dari suatu relasi ke dalam bentuk gambar arah panah yang menyatakan hubungan antara anggota himpunan A dengan anggota himpunan B.
Misalnya, ada 4 orang anak yaitu Ali, Siti, Amir dan Rizki. Mereka diminta untuk menyebutkan warna favorit mereka. Ali menyukai warna merah, Siti menyukai warna ungu, Amir menyukai warna hitam, dan Rizki menyukai warna merah. Dari hasil uraian tersebut, terdapat dua buah himpunan.
Himpunan pertama adalah himpunan anak, kita sebut himpunan A dan himpunan yang kedua adalah himpunan warna, kita sebut himpunan B. Hubungan antara himpunan A dan himpunan B dapat di ilustrasikan dengan diagram panah seperti berikut:

Jadi, dapat disimpulkan bahwa diagram panah di atas merupakan relasi antara anak dengan warna yang mereka sukai. Relasi antara kedua himpunan tersebut dapat dinyatakan dengan panah-panah yang memasangkan anggota himpunan A dengan anggota himpunan B.
Himpunan Pasangan Berurutan
Selain dengan diagram panah, suatu relasi juga dapat dinyatakan dengan menggunakan himpunan pasangan berurutan. Caranya dengan memasangkan himpunan A dengan himpunan B secara berurutan. Kita dapat mengambil contoh dari contoh diagram panah tadi.
- Ali menyukai warna merah
- Siti menyukai warna ungu
- Amir menyukai warna hitam
- Rizki menyukai warna merah
Dari uraian di atas kita dapat menyatakan relasinya dengan himpunan pasangan berurutan seperti berikut:
(Ali, merah), (Siti, ungu), (Amir, hitam), (Rizki, merah).
Jadi, relasi antara himpunan A dengan himpunan B dinyatakan sebagai himpunan pasangan berurutan (x,y) dengan x ∈ A dan y ∈ B.
Diagram Cartesius
Menyatakan relasi antara dua himpunan dari pasangan berurutan yang kemudian dituliskan dalam bentuk dot (titik-titik). Contoh dari relasi antara anak dengan warna kesukaannya yaitu himpunan A = {Ali, Siti, Amir, Rizki} dan himpunan B = {merah, ungu, hitam}, dapat digambarkan dalam bentuk diagram Cartesius seperti di bawah ini:

Jenis – jenis Relasi
Relasi Refleksif
Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen A berhubungan dengan dirinya.
Contoh relasi yang memiliki sifat seperti ini adalah relasi “x selalu bersama y.”, dengan x dan y adalah anggota himpunan seluruh manusia. Jelas sekali bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.
Relasi Irefleksif
Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri.
Contoh relasi irefleksif adalah relasi “x mampu mencukur rambut y dengan rapi sempurna.”, dengan x dan y adalah setiap pemotong rambut. Diandaikan bahwa setiap orang hanya dapat mencukur rambut orang lain dengan rapi sempurna, maka relasi ini adalah irefleksif, karena tidak ada seorang tukang cukur a yang mampu mencukur rambutnya sendiri.
Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.
Relasi Simetrik
Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota A berhubungan satu sama lain. Dengan kata lain, jika a terhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik.
Sebuah relasi “ genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.
Relasi Anti-simetrik
Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsi a dan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.
Relasi Transitif
Sebuah relasi disebut transitif jika memiliki sifat, jika a berhubungan dengan b, dan b berhubungan dengan c, maka a berhubungan dengan c secara langsung.
Sebagai contoh, relasi dua transitif. Misalnya untuk 5, 6, dan 7, berlaku 5 < 6, 6 < 7, dan 5 < 7
Sebuah relasi disebut sebagai relasi ekivalen jika relasi tersebut bersifat:
- Refleksif
- Simetrik, dan
- Transitif
Orde parsial adalah relasi yang bersifat:
- Refleksif
- Anti-simetrik, dan
- Transitif
Contoh soal Relasi dan penyelesaiannya :
Misalkan A adalah himpunan yang anggotanya Anto, Andi, Yudi, Ani, Mila, dan Yanti. Dimana Anto, Andi, dan Yudi berjenis kelamin laki-laki, dan Ani, Mila, dan Yanti berjanis kelamin perempuan. Apakah himpunan A merupakan relasi ekuivalen ?
Jawab :
Untuk membuktikan himpunan A merupakan relasi ekuivalen harus memenihi ke-3 sifat yaitu refleksif,simetri dan transitif
- sifat refleksif
anto ~ anto , berelasi dengan dirinya sendiri karena jenis kelaminnya laki-laki
- sifat simetri
anto ~ andi
andi ~ anto , anto berelasi dengan andi dan andi berelasi dengan anto karena jenis kelaminnya sama.
- sifat transitif
Mila ~ Ani
Ani ~ Yanti
Mila ~ Yanti
Mila berelasi dengan Ani dan Ani berelasi dengan Yanti maka otomatis Mila berelasi dengan Yanti karena jenis kelaminnya sama
kesimpulannya jadi himpunan A merupakan relasi ekuivalen karena memenuhi ke-3 sifat dan sudah mempunyai relasi yaitu jenis kelamin yang sama.
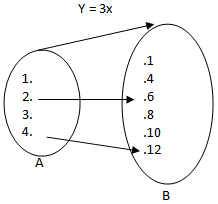
- A = { x│x ≤ 4,x ϵ asli }
B = { y│2 ≤ y ≤ 12,y ϵ genap }
Tentukan relasi dari A ke B yang menyebabkan y = 3x
Jawab :
A = daerah asal (domain)
B = daerah hasil (kodomain)
Yang di tuju anak panah di sebut daerah hasil (range).Lima orang siswa memilih kegiatan masing-masing. Adit dengan basket , Candra dengan karate, Yoseph dengan voli, Ilham dengan tenis meja dan Joni dengan judo. Tuliskan relasi tersebut dengan himpunan pasangan berurutan!
Jawab :
{(Adit,basket),(Candra,karate),(Yoseph,voli),(Ilham,tenis meja),(Joni,judo)}