Definisi, Rumus, Sifat, Penggolongan dari Segitiga

Berikut ini penjelasan mengenai segitiga atau triangel berisi rumus luas dan keliling dan sifat-sifat dan penggolangan segitiga berdasar panjang sisi dan sudut. Seperti segitiga sama kaki, sama sisi, sembarang dan berdasar pada sudut seperti segitiga siku-siku, lancip dan tumpul. Dan terakhir sedikit menyinggung tentang pythagoras

Segitiga adalah bangun datar yang dibuat dari tiga sisi yang berupa garis lurus yang saling saling berpotongan dan tiga sudut yang tidak segaris.

Matematikawan Euclid yang hidup sekitar tahun 300 SM menemukan bahwa jumlah ketiga sudut di suatu segitiga pada bidang datar adalah 180°. Hal ini memungkinkan kita menghitung besarnya salah satu sudut bila dua sudut lainnya sudah diketahui.

Bagian Bagian pada Segitiga

Setiap bangun datar pastilah memiliki bagian- bagian untuk membentuk bangun tersebut.Berikut bagian – bagian pada segitiga :

Sudut adalah pertemuan antara garis lurus yang bertemu pada satu titik.
Sudut luar sebuah segitiga adalah sudut yang terbentuk oleh sisi segitiga dan perpanjangan sisi lainnya dalam segitiga tersebut. sedangkanSudut dalam segitiga adalah sudut yang tebentuk didalam segitiga melalui pertemuan setiap garis.
Garis lurus adalah garis penghubung terpendek antara dua titik yang tidak bertepatan. Sedangkan, garis tinggi pada suatu sisi segitiga adalah garis yang ditarik dari sebuah titik sudut segitiga dan tegak lurus sisi di depannya.
Garis bagi adalah garis yang ditarik dari titik sudut segitiga dan membagi sudut tersebut menjadi dua sama besar. Sedangkan, garis sumbu adalah garis yang tegak lurus dan melalui titik tengah sisi tersebut.
Dan, garis berat adalah garis yang menghubungkan titik sudut di hadapan sisi itu dengan titik tengah sisi itu.

Jenis – jenis Segitiga

Segitiga dapat diklarifikasikan kedalam dua jenis yaitu segitiga menurut panjang sisinya dan menurut besar sudutnya.

Segitiga Berdasarkan Panjang Sisi

pembagian bentuk segitiga menurut panjang sisi di bagi menjadi 3 jenis yaitu

Segitiga **Sama Kaki (Isosceles triangle)**

adalah segitiga yang dua dari tiga sisinya sama panjang, dan mempunyai dua sudut yang sama besar. Segitiga sama kaki dibentuk oleh dua buah segitiga siku-siku yang kongruen dengan menghimpitkan kedua sisi yang sama panjangnya.

Affiliate Banner Unlimited Hosting Indonesia

Sifat – sifat Segitiga Sama Kaki

Berikut adalah beberapa sifat asegitiga sama kaki

Segitiga sama kaki mempunyai dua buah sisi yang sama panjang sebagai kaki segitiga
Segitiga sama kaki mempunyai satu buah sumbu simetri,
Mempunyai dua sudut yang besarnya sama yaitu sudut yang berhadapan dengan sisi yang sama panjang.
Segitiga sama kaki merupakan salah satu bangun simetri lipat yang dapat menempati bingkainya dengan dua cara

Rumus Segitiga Sama Kaki

Keliling

$\Large Keliling = \overline{AB}+\overline{BC}+\overline{CA}$

$\Huge Keliling = a + b +c$

$\Large Keliling = a + 2b$

Luas

h = \sqrt{b^{2}-\left ( \frac{1}{2}a^{2} \right )}

**Segitiga Sama Sisi (Equilateral Triangle)**

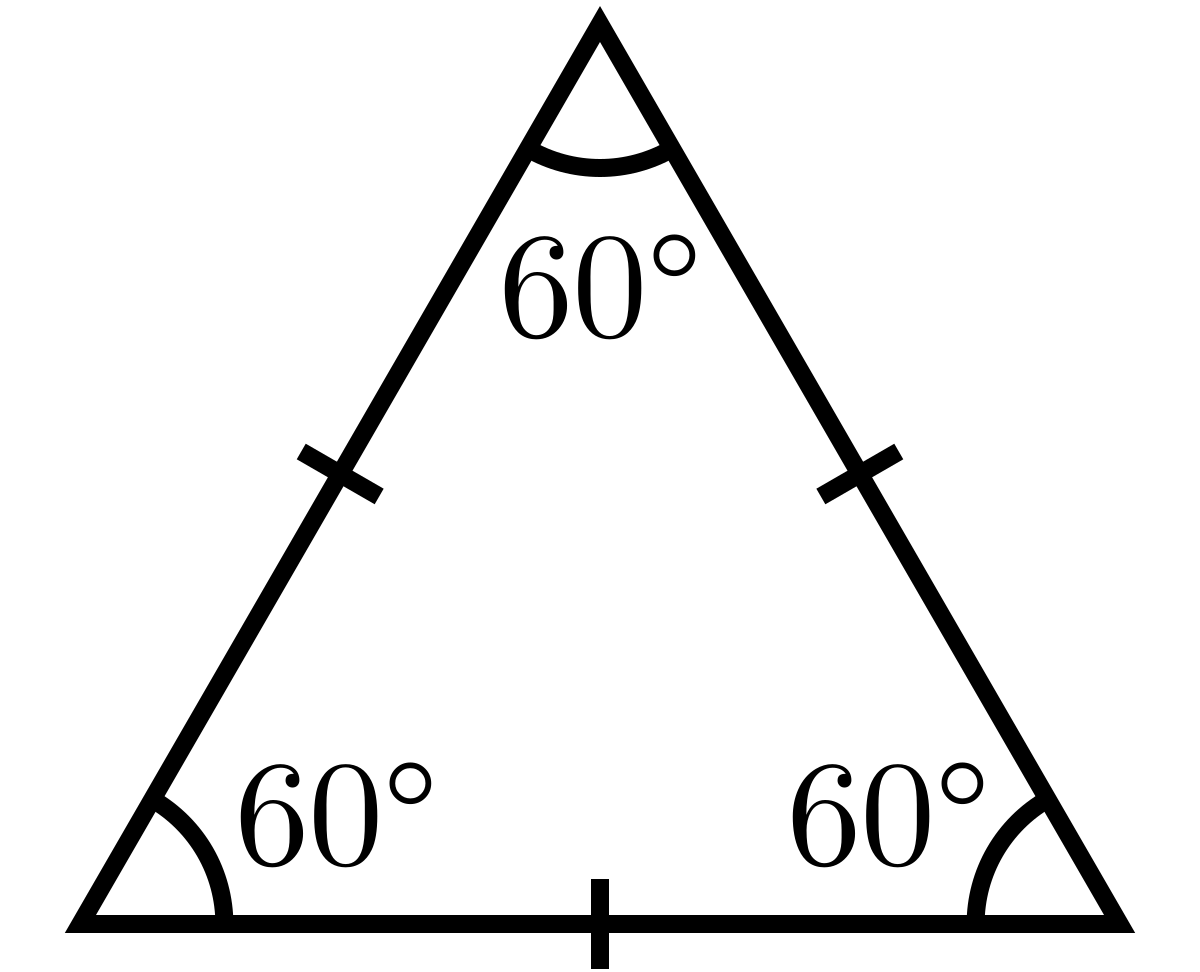
Segitiga sama sisi adalah jenis segitiga yang ketiga sisi mempunyai ukuran yang sama panjang. Karena sisinya yang sama panjang, setiap titik sudut pada segitiga sama sisi mempunyai besar 60°.

Rumus segitiga sama sisi mempunyai formula yang istimewa, yang merupakan aplikasi dari teorema Pythagoras.

Segitiga sama sisi - Wikipedia bahasa Indonesia, ensiklopedia bebas

Sifat – sifat Segitiga Sama Sisi

Berikut sifat – sifat segitiga sama sisi

Semua sisinya sama panjang.
Semua sudutnya membentuk sudut 60°.
Segitiga sama sisi mempunyai 3 sumbu simetri.
Sumbu simetri dapat digunakan sebagai tinggi segitiga.

Rumus Segitiga Sama Sisi

Keliling

$\Large Keliling = \overline{AB}+\overline{BC}+\overline{CA}$

$\Huge Keliling = a + b +c$

$\Large Keliling = 3\cdot s$

Luas

Untuk mencari luas segitiga sama sisi pertama kita harus mencari tinggi segitiga tersebut. Apabila di soal telah diketahhui tingginya maka lanjut ke rumus luas dengan a adalah panjang sisi segitiga

Adapun langkah – langkah mencari luas sebagai berikut

t = \sqrt{a^{2}-\left(\frac{a}{2}\right)^{2}}

**Segitiga Sembarang (Scalene)**

Segitiga Sembarang yaitu sebuah bangun datar yang dilihat dari panjang sisi – sisinya sehingga dapat dibilang masih kerabat dekat dengan segitiga sama sisi dan sama kaki tetapi sifatnya berbeda.

Sifat – sifat Segitiga Sembarang

Berikut sifat – sifat segitiga sembarang

Ketiga sisinya tidak sama panjang
Ketiga sudut besarnya berbeda
Tidak mempunyai simetri lipat
Simetri putar hanya ada satu
Jumlah ketiga sudutnya adalah 180⁰
Tidak memiliki sumbu simetri

Selain sifat – sifat diatas segitiga sembarang mempunyai banyak jenis tetapi segitiga sembarang dibagi menjadi 3 yang utama yaitu :

Pertama, Segitiga sembarang memiliki 3 buah sisi yang tidak sama panjang.
Kedua, Segitiga sembarang tidak memiliki simetri lipat tetapi memiliki 1 buah simetri putar.
Ketiga, Segitiga sembarang memiliki 3 sudut, ketiga sudutnya mempunyai besar yang berbeda.

kumpulan materi pelajaran dan contoh soal 6: Rumus Luas Segitiga ...

Rumus Segitiga Sembarang

Keliling

$\Large Keliling = \overline{AB}+\overline{BC}+\overline{CA}$

$\Large Keliling = a + b +c$

Luas

Luas segitiga sembarang dicari dengan mendapat s (setengah keliling ) dari segitiga tersebut. Berikut langkah langkah mencari luas segitiga sembarang

s =\frac{ \overline{AB}+\overline{BC}+\overline{CA}}{2}

Segitiga Berdsarkan Besar Sudut

Sedangkan, berdasarkan besar sudut segitiga dibagi menjadi 3 jenis yaitu

**Segitiga Siku-siku (Right Triangle)**

Segitiga siku-siku adalah segitiga yang satu sudutnya tepat sebesar 90° (tegak lurus atau siku-siku). Dalam bahasa Inggris disebut right triangle atau or right-angled triangle, dan dulu disebut rectangled triangle.

Sisi yang berhadapan dengan sudut tegak lurus tersebut disebut hipotenusa ( garis miring ), merupakan sisi terpanjang pada segitiga siku-siku.

Segitiga siku-siku mematuhi teorema Pythagora jumlah kuadrat dari panjang kedua kaki sama dengan kuadrat panjang hipotenusa a² + b² = c², Dimana a dan b adalah panjang masing – masing kaki dan c adalah panjang hipotenusa.

Sifat – sifat Segitiga Siku – siku

Jumlah sudut-sudut yang bukan siku-siku pasti 90°.
Jika kaki-kaki segitiga siku-siku sama panjang, maka sudut yang berseberangan dengan kaki-kaki tersebut akan sama besarnya. Dengan demikian karena sifat pertama di atas, maka sudutnya pasti 45°. Dengan teorema Pythagoras, panjang hipotenusa adalah panjang kaki dikali √2.
Di segitiga siku-siku jika besar sudut lainnya 30° dan 60°, maka panjang hipotenusa dua kali panjang kaki terpendek dan panjang kaki yang lebih panjang sama dengan panjang kaki yang lebih pendek dikali √3

Rumus Segitiga Siku – siku

les privat | bimbel Semarang | TK/SD/SMP/SMA/UMUM/STAN

Keliling

$\Large Keliling = \overline{AB}+\overline{BC}+\overline{CA}$

$\Large Keliling = a + b +c$

Luas

Pythagoras

Rumus pythagoras dengan nama lain yaitu teorema pythagoras ataupun dalil pythagoras. Dibawah ini adalah bunyi dari dalil pythagoras atau teorema pythagoras.

“Di dalam segitiga siku siku, ukuran sisi terpanjang atau sisi miring sama dengan kuadrat dari sisi lainnya”

Rumus pythagoras menggambarkan hubungan yang terjadi antara sisi dalam segitiga siku siku. Hasil panjang sisi miringnya adalah jumlah dari kuadrat kedua sisi lainnya.

**Segitiga Tumpul (Obtuse Triangle)**

Segitiga Tumpul adalah sebuah segitiga yang memiliki satu titik sudut yang besarnya lebih dari 90 derajat. Kenapa hanya satu sudut? Alasannya karena tidak mungkin membuat segitiga yang memiliki lebih dari satu sudut yang besarnya > 90 derajat.

Karena da satu sudut yang nilainya 125 derajat (lebih dari 90) maka segitiga di atas disebut segitiga tumpul.

**Segitiga Lancip (Acute Triangle)**

Lawan dari segitiga tumpul adalah segitiga lancip.

Ciri-ciri segitiga ini adalah semua sudutnya kurang dari 90 derajat.

$h = \sqrt{b^{2}-\left ( \frac{1}{2}a^{2} \right )}$	$Luas = \frac{1}{2}\cdot a\cdot h$
$= \sqrt{b^{2}-\frac{1}{4}a^{2}}$	$Luas = \frac{1}{2}\cdot a\cdot \frac{1}{2}\sqrt{4b^{2}-a^{2}}$
$= \sqrt{\frac{4b^{2}-a^{2}}{4}}$	$Luas = \frac{1}{4}a\sqrt{4b^{2}-a^{2}}$
$h = \frac{1}{2}\sqrt{4b^{2}-a^{2}}$

$t = \sqrt{a^{2}-\left(\frac{a}{2}\right)^{2}}$	$Luas = \frac{1}{2}\cdot a\cdot t$
$t = \sqrt{a^{2}-\frac{1}{4}a^{2}}$	$Luas = \frac{1}{2}\cdot a\cdot \left ( \frac{1}{2}a\sqrt{3} \right )$
$= \sqrt{\frac{3}{4}a^{2}}$	$Luas = \frac{1}{4}a^{2}\sqrt{3}$
$t = \frac{1}{2}\cdot a\cdot \sqrt{3}$

Definisi, Rumus, Sifat, Penggolongan dari Segitiga

Bagian Bagian pada Segitiga